#09 EDA(with Pandas)

EDA(Exploratory Data Analysis, 탐색적 자료 분석)

• 데이터를 분석하고 결과를 도출하는 과정에 있어서 지속적으로 해당 데이터에 대한 탐색과 이해를 가져야 한다는 의미

데이터 종류

• 수치형 데이터
  • 연속형 : 일정범위 안에서 어떤 값도 취할 수 있는 실수형 데이터 ex) 온도, 키, 풍속, 운임료
  • 이산형 : 횟수 같은 정수형 데이터 ex) 사건 발생 빈도수, 방 개수, 부모자식 수
• 범주형 데이터 : 가능한 범주안의 값만 취할 수 있는 데이터
  • 명목형 : 성별(남, 여), 전공(경영정보학, 인문학, 사회학 등), 장르(스릴러, 로맨스, 공포 등)
  • 순서형 : 영화평점(1, 2, 3, 4, 5), 직급(사원, 대리, 과장, 차장, 부장)

# pandas, numpy import, google colab drive mount
import pandas as pd
import numpy as np
from google.colab import drive
drive.mount("/content/drive/")

• feautres(= 독립변수 = 설명변수) : 학습 데이터의 특성(머신러닝 task에선 feature를 잘 추가하는게 핵심)
• class(= label = target = 종속변수) : 정답 데이터

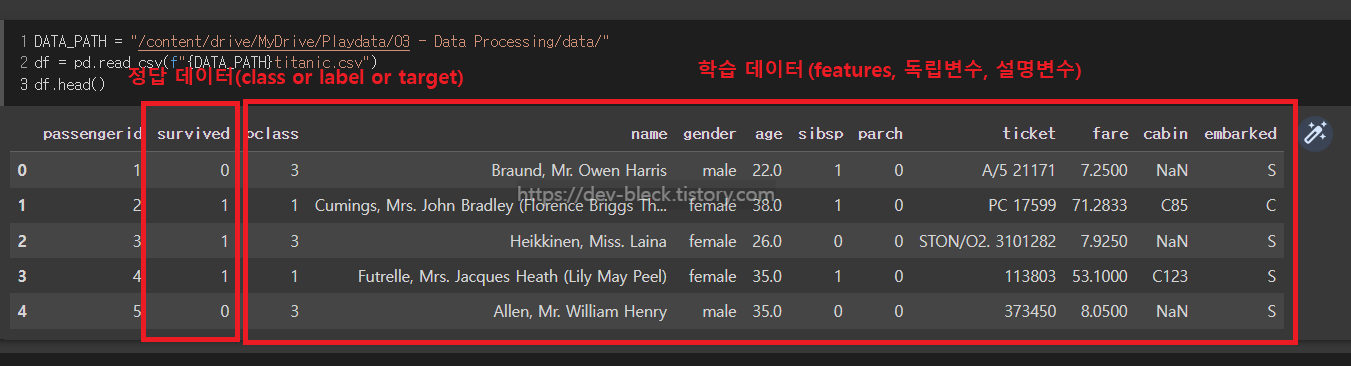
DATA_PATH = "/content/drive/MyDrive/ ~ /"
df = pd.read_csv(f"{DATA_PATH}titanic.csv") # drive 경로에 있는 titanic dataset 불러오기

df.info() # 처음에 정보부터 확인 ex) 결측치가 많네 => 어떻게 처리해야겠다
>>> <class 'pandas.core.frame.DataFrame'>
    RangeIndex: 1309 entries, 0 to 1308
    Data columns (total 12 columns):
     #   Column       Non-Null Count  Dtype  
    ---  ------       --------------  -----  
     0   passengerid  1309 non-null   int64  
     1   survived     1309 non-null   int64  
     2   pclass       1309 non-null   int64  
     3   name         1309 non-null   object 
     4   gender       1309 non-null   object 
     5   age          1046 non-null   float64
     6   sibsp        1309 non-null   int64  
     7   parch        1309 non-null   int64  
     8   ticket       1309 non-null   object 
     9   fare         1308 non-null   float64
     10  cabin        295 non-null    object 
     11  embarked     1307 non-null   object 
    dtypes: float64(2), int64(5), object(5)
    memory usage: 122.8+ KB

수치형 데이터 분석

# 총합
df["fare"].sum()
>>> 43550.4869

# 평균
df["fare"].mean()
>>> 33.29547928134557

# 중앙값
df["fare"].median()
>>> 14.4542 # 평균과 중앙값의 차이가 많이 남

# 분산
df["fare"].var()
>>> 2678.959737892891

# 표준편차
df["fare"].std()
>>> 51.75866823917411 # 표준편차와 중앙값의 차이가 많이남. => 분포가 매우 퍼져있다

# 분위수 계산
df["fare"].quantile([0.25, 0.5, 0.75, 1]) # 데이터의 75%가 평균에도 못 미침
>>> 0.25      7.8958
    0.50     14.4542
    0.75     31.2750
    1.00    512.3292
    Name: fare, dtype: float64

df["fare"].quantile([0.5, 0.95])
>>> 0.50     14.4542
    0.95    133.6500
    Name: fare, dtype: float64

왜도(= 비대칭도, Skewness)

• 데이터 분포의 비대칭 정도를 나타내는 통계량
• 분포가 오른쪽으로 치우쳐져 있고, 왼쪽으로 긴 꼬리르 가진 경우 왜도는 음수
• 분포가 왼쪽으로 치우쳐져 있고, 오른쪽으로 긴 꼬리를 가진 경우 왜도는 양수
• 정규분포와 같이 좌우 대칭인 경우 왜도는 0에 가까워짐

df["fare"].skew() # 왜도 => 양수
>>> 4.367709134122922

상관계수

• 칼 피어슨(Karl Pearson)이 개발
• 두 개의 수치형 변수의 변화가 연관되는 정도
• +1 ~ -1 사이의 값을 가짐
• +1에 가까울 수록 양의 상관관계
• -1에 가까울 수록 음의 상관관계
• 0에 가까울 수록 상관관계 X

cols = ["survived", "age", "sibsp", "parch", "fare"]
df[cols].corr()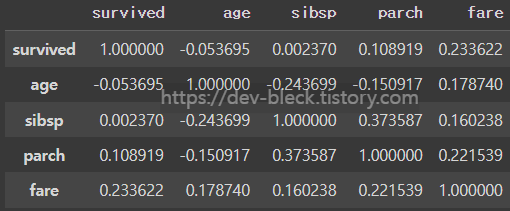

df[cols].corr() 출력

범주형 데이터 분석

# 고유값
df["embarked"].unique()
>>> array(['S', 'C', 'Q', nan], dtype=object)

# 고유값 개수
df["embarked"].nunique() # "고유값이 3개 밖에 없으니 one-hot 인코딩을 해야겠다" 같은 판단이 가능
>>> 3

# 최빈값
df["embaarked"].mode()
>>> 0    S
    dtype: object

# 범주별 개수
df["embarked"].valus_counts()
>>> S    914
    C    270
    Q    123
    Name: embarked, dtype: int64

df["embarked"].value_counts(normalize = True) # normalize = True => 정규화
>>> S    0.699311
    C    0.206580
    Q    0.094109
    Name: embarked, dtype: float64

두 범주형 데이터 간 관계

pd.crosstab(df["gender"], df["survived"], margins = True) # magrins = True : 소계 출력

pd.crosstab(df["gender"], df["survived"], margins = True) 출력

# index 기준으로 정규화
pd.crosstab(df["gender"], df["survived"], margins = True. normalize = "index")

pd.crosstab(df["gender"], df["survived"], margins = True, normalize = "index") 출력

 

# columns 기준으로 정규화
pd.crosstab(df["gender"], df["survived"], margins = True. normalize = "columns")

pd.crosstab(df["gender"], df["survived"], margins = True, normalize = "columns") 출력